დიფერენციალური აღრიცხვა

წარმოებულის გეომეტრიული შინაარსი. y = f (x) ფუნქციის გრაფიკზე ირჩევენ აბსცისას x0 და გამოითვლიან შესაბამის ორდინატას y = f (x0). x0 წერტილის მიდამოში ირჩევენ ნებისმიერ წერტილს x0 + Δ x და ფუნქციის გრაფიკის შესაბამის A და B წერტილებზე გაავლებენ AB მკვეთს. როცა აბსცისის ნაზრდი Δ x = x - x0 მისწრაფვის ნულისკენ (ანუ როცა x წერტილი მიისწრაფვის x0 წერტილისკენ), AB მკვეთი მიისწრაფვის AC მხებისკენ. AC მხების დახრის კუთხის ტანგენსი არის y = f (x) ფუნქციის წარმოებული x0 წერტილში.

დიფერენციალური აღრიცხვა, მათემატიკის დარგი, რ-იც შეისწავლის ფუნქციის წარმოებულებს, დიფერენციალებსა და მათი გამოყენების ხერხებს.

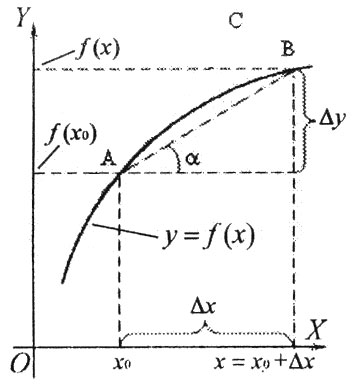
დ. ა. ემყარება მათემატიკის უმნიშვნელოვანეს ცნებებს (ნამდვილი რიცხვი, ფუნქცია, ზღვარი, უწყვეტობა). დ. ა-ის ცენტრ. ცნებებია წარმოებული და დიფერენციალი. y = f (x) ფუნქციის წარმოებული ხ წერტილში [აღინიშნება y', f '(x) ან dy/dx სიმბოლოებით] ეწოდება ფუნქციის ნაზრდისა და არგუმენტის ნაზრდის შეფარდების ზღვარს (თუ კი ის არსებობს), როცა არგუმენტის ნაზრდი ნებისმიერად მიისწრაფვის ნულისაკენ. წარმოებულის მოძებნის ოპერაციას გაწარმოება ეწოდება. თუ f '(x) ფუნქციას, თავის მხრივ, აქვს წარმოებული, მაშინ ამ უკანასკნელს y = f (x) ფუნქციის მეორე რიგის წარმოებულს უწოდებენ და მას y, f (x) ან d2y/dx2 სიმბოლოებით აღნიშნავენ. ანალოგიურად განსაზღვრავენ უფრო მაღალი რიგის წარმოებულებსაც. dy = f '(x)Δx წრფივ ფუნქციას უწოდებენ y = f (x) ფუნქციის დიფერენციალს x0 წერტილში. დამოუკიდებელი x ცვლადის დიფერენციალი ემთხვევა მის ნაზრდს, dx = Δx, ამიტომ dy = f '(x)dx, ე. ი. f '(x) = dy/dx.

წარმოებულის ცნება წარმოიშვა ბუნებისმეტყველებისა და მათემატიკის მრავალი ამოცანიდან. მ. შ. უმნიშვნელოვანესია წერტილის მოძრაობის მყისი სიჩქარის განსაზღვრა და წირის მხების აგება.

დ. ა-ის ჩამოყალიბება დამოუკიდებელ მათ. დისციპლინად დაკავშირებულია ინგლ. მეცნიერის ი. ნიუტონისა და გერმ. მეცნიერის გ. ლაიბნიცის სახელებთან (XVII ს. II ნახ.). მათ ჩამოაყალიბეს დ. ა-ის ძირითადი დებულებები და მიუთითეს დიფერენცირებისა და ინტეგრების ურთიერთდამოკიდებულებაზე. იმ დროიდან დ. ა. ვითარდება ინტეგრალურ აღრიცხვასთან ერთად და ორივე შეადგენს მათემატიკური ანალიზის (უსასრულოდ მცირეთა აღრიცხვის) ძირითად ნაწილს.

დ. ა-ის შემდგომ განვითარებაში დიდი როლი შეასრულა ლ. ეილერისა და ჟ. ლაგრანჟის შრომებმა (XVIII ს.). ეილერმა პირველმა ჩამოაყალიბა დ. ა., როგორც გეომეტრიისა და მექანიკისაგან დამოუკიდებელი ანალიზური დისციპლინა.

XIX ს-ში ზღვართა თეორიის საფუძველზე გადაწყდა დ. ა-ის დაფუძნების ამოცანა. ამ საქმეში დიდი წვლილი მიუძღვით ფრანგ, ჩეხ და გერმ. მათემატიკოსებს: ო. კოშის, ბ. ბოლცანოს, კ. ფ. გაუსს, კ. ვაიერშტრასს.

დ. ა-ის საწყისი ცნებების უფრო ღრმა ანალიზი დაკავშირებულია სიმრავლეთა თეორიისა და ნამდვილი ცვლადის ფუნქციათა თეორიის განვითარებასთან (XIX ს. დასასრ. და XX ს. დასაწყ.).

დ. ა-ის პირველი სახელმძღვანელო ქართ. ენაზე შეადგინა ა. რაზმაძემ (დაიბეჭდა თბილისში 1920).

ლიტ: გ ო კ ი ე ლ ი ლ., დიფერენციალური აღრიცხვა, ტფ., 1932; რ ა ზ მ ა ძ ე ა., მათემატიკური ანალიზის კურსი, ტ. 1 – შესავალი, ტფ., 1920; ქ ა რ ც ი ვ ა ძ ე ი., მათემატიკური ანალიზი, ტ. 1, თბ., 1981; ხ ა რ ა ძ ე ა., ჭ ე ლ ი ძ ე ვ., ხ ვ ე დ ე ლ ი ძ ე ბ., ქ ა რ ც ი ვ ა ძ ე ი., მათემატიკური ანალიზის კურსი, ტ. 1–2, თბ., 1963–68.